Круг и множество точекЗадача:На плоскости заданы множество точек М и круг. Выбрать из М две различные точки так, чтобы наименьшим образом различались количества точек в круге, лежащие по разные стороны от прямой, проходящей через эти точки.Описание:Решение задачи можно разбить на несколько пунктов:1) выборка двух точек из n без повторений реализована циклами for i:= 1 to n-1 do for j:= i+1 to n do begin ... end;2) внутри этого цикла производится перебор всех точек, и выясняется лежит ли проверяемая точка внутри круга (условие (x-rx)2+(y-ry)2 > r2 означает, что расстояние от точки до центра круга меньше его радиуса). Если точка внутри круга подставляем её координаты( x и y ) в уравнение прямой  где x1,y1,x2,y2 - координаты первой и второй выбранных выше точек соответственно. Подставляем x и y: если 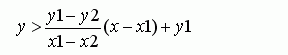 , то точка находиться выше прямой , то точка находиться выше прямойесли  , то ниже прямой. , то ниже прямой.Может оказаться так, что точки имеют одинаковую координату по x, поэтому в уравнении получиться деление на ноль. Поэтому перед подстановкой в неравенство(уравнение прямой), сравним абсциссы точек, и если они равны, все точки будут лежать либо справа либо слева от прямой. Чтобы выяснить, где лежит каждая проверяемая точка будем сравнивать первую координату точки с первой координатой любой из двух выбранных точек(в нашем примере сравнивается с координатой первой точки). 3) После каждого сравнения увеличиваем счётчики high - для подсчёта точек выше прямой или справа и счётчик low - для подсчёта точек ниже прямой и ,соответственно, слева от неё. Каждый раз найдя решение лучше предыдущего сохраняем его в переменных res, t1, t2. Код: | ||
program Krug;
const
n = 5; {число точек}
var
i,j,t,r,rx,ry,high,low,res: integer; {i,j,t - счётчики}
M: array[1..n,1..2] of integer;
t1,t2: integer; {в них запишем номера двух точек, - решение задачи}
Begin
rx:= 0; {x-координата центра круга}
ry:= 0; {y-координата центра круга}
r:= 8; {радиус круга}
Randomize; {координаты точек задаём пройзвольно}
for i:= 1 to n do begin
M[i,1]:= Random(21)-10; {из диапазона [-10,10]}
M[i,2]:= Random(21)-10;
end;
for i:= 1 to n do begin {вывод координат точек на экран}
Write(M[i,1]:3,' ',M[i,2]:3);
Writeln;
end;
res:= n+1; {инициализация просто большим числом}
for i:= 1 to n do
if sqr(M[i,1]-rx)+sqr(M[i,2]-ry) > sqr(r) then inc(j); {в j считаем точки вне круга}
if j = n then begin
Writeln('Все точки вне круга!');
Readln;
Exit;
end;
for i:= 1 to n-1 do {выборка двух точек из n без повторений}
for j:= i+1 to n do begin {-//-}
high:= 0; {начальные условия: high - для подсчёта точек выше прямой или справа, если}
low:= 0; {прямая параллельна Oy; low - для подсчёта точек ниже и ,соответственно, слева}
for t:= 1 to n do begin {перебираем все точки}
if sqr(M[t,1]-rx)+sqr(M[t,2]-ry) < sqr(r) then {которые внутри круга}
begin
if (M[i,1]=M[j,1]) and (M[t,1] > M[i,1]) then inc(high); {прямая||Oy, точки справа}
if (M[i,1]=M[j,1]) and (M[t,1] < M[i,1]) then inc(low); {прямая||Oy, точки слева}
if (M[i,1] <> M[j,1]) then begin {прямая не||Oy, подставляем координаты в уравнение прямой}
if M[t,2] > ((M[i,2]-M[j,2])/(M[i,1]-M[j,1]))*(M[t,1]-M[i,1])+M[i,2] then inc(high);
if M[t,2] < ((M[i,2]-M[j,2])/(M[i,1]-M[j,1]))*(M[t,1]-M[i,1])+M[i,2] then inc(low);
end;
end;
end;
if res > abs(high - low) then begin {вычисляем разницу high - low по модулю}
res:= abs(high - low); {если меньше результата, полученного ранее}
t1:= i; {эти две точки будут новым решением}
t2:= j;
end;
end;
Writeln;
Writeln(res); {вывод разницы в количестве точек по разные стороны от прямой}
Writeln(M[t1,1]:3,' ',M[t1,2]:3); {и самих точек на экран}
Writeln(M[t2,1]:3,' ',M[t2,2]:3);
Readln;
End.
|
||